カイ二乗分布

概要

文系プログラマが数式アレルギーを治す為に、中学〜高校レベルの知識でもわかる数式を、プログラムのコードに直す作業を黙々と続ける企画。

ソースコードはJuliaを利用。前回、pycallを使ってもなんとかならなかったJuliaを利用。そのうち良いライブラリが生まれるはず。きっと。（人任せ）

今回のテーマはカイ二乗分布。検定の際にはお世話になっております。

数式

式はWikipediaのカイ二乗分布を参考にした。

http://ja.wikipedia.org/wiki/%E3%82%AB%E3%82%A4%E4%BA%8C%E4%B9%97%E5%88%86%E5%B8%83

こんな感じ。

$f(x;k)=\genfrac{}{}{0.1ex}{}{{\left(\genfrac{}{}{0.1ex}{}{1}{2}\right)}^{k/2}}{\Gamma \left(\genfrac{}{}{0.1ex}{}{k}{2}\right)}{x}^{\genfrac{}{}{0.1ex}{}{k}{2}-1}{\mathrm{e}}^{\genfrac{}{}{0.1ex}{}{-x}{2}}$

# 自分用メモ
$ f( x;k ) = \frac { (\frac {1} {2}) ^ {k/2} } { \Gamma( \frac {k} {2} ) } x ^ { \frac {k} {2} - 1} \mathrm{e} ^ { \frac {-x} {2} } $

このくらいの複雑さになってくると、latexの記法に直すだけでもちょこちょこ間違える。コードにしたらさらに間違える。

SciPy先生で答え合わせできるのはとてもありがたい。

数式の解説

f(x;k)はxとkを引数に取る関数。

kには自由度を入れる。可変。今回は1〜10くらいで計算する予定。

Γ（ガンマ）はガンマ関数。今回はJuliaのgamma関数をそのまま使う。k/2のガンマ関数とか自前で出すとこれより難しいし。

eはネイピア数。

コードに直す

じゃ、いつものように断片をJuliaのコードに直してみる。まｍずは前半の((1/2)^k/2)/Γ(k/2)のあたり。

((1/2) ^ (k/2) ) / gamma( k/2 )

次、残りの部分。

(x ^ (k/2 - 1)) * (e ^ (-x / 2))

合わせるとこんな感じ。

f(x, k) = ((1/2) ^ (k/2) ) / gamma( k/2 ) * (x ^ (k/2 - 1)) * (e ^ (-x / 2))

試しにk=1とk=2の時でxが0〜10の間をplotしてみる。

# k=1の関数
f1(x) = f(x, 1)
# k=2
f2(x) = f(x, 2)
# k=3
f3(x) = f(x, 3)

# plot
import Winston
Winston.hold(true)
Winston.fplot( f1, [0, 10], color="red" )
Winston.fplot( f2, [0, 10], color="blue" )
Winston.fplot( f3, [0, 10], color="green" )

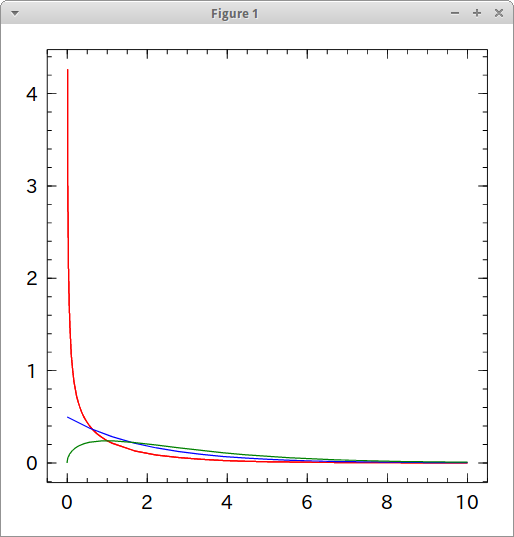
知ってるグラフより背が高いな。自由度1でxが0の場合は、解がInfinityになってる。そうなるんだっけか。

SciPy先生で答え合わせ

じゃ、今回書いた処理が合ってるか、答え合わせ。

まずは自作の関数でいくつか数値を出してみる。

f(0, 0)
  #=> NaN

f(1, 1)
  #=> 0.24197072451914337

f(2, 1.5)
  #=> 0.1501038138420087

f(3, 0.5)
  #=> 0.02270276544056991

同じ数値でSciPyでの結果を見てみる。

import scipy as sp

sp.stats.chi2.pdf( 0, 0 )
  #=> nan

sp.stats.chi2.pdf( 1, 1 )
  #=> 0.24197072451914337

sp.stats.chi2.pdf( 2, 1.5 )
  #=> 0.15010381384200866

sp.stats.chi2.pdf( 2, 1.5 )
  #=> 0.022702765440569903

桁が少し違うけど数字は合ってるね。良かった。

注意事項としてこれはXが0以上の時の関数になる。本当は0より小さい場合は0が返るようにif文1個足さないといけない。