ネイピア数
概要
文系プログラマが数式アレルギーを治す為に、中学〜高校レベルの知識でもわかる数式を、プログラムのコードに直す作業を黙々と続ける企画。
ソースコードはJuliaを利用。数式をコードに直すという用途ではどの言語よりも便利な気がするJuliaを利用。
今回のテーマはネイピア数。うちのトイレットペーパーはネピア。
@Versions Julia0.3.3
数式
式はWikipediaのネイピア数とかを参考にした。
http://ja.wikipedia.org/wiki/%E3%83%8D%E3%82%A4%E3%83%94%E3%82%A2%E6%95%B0
今回はこんな感じの数式を扱うことにする。厳密に計算するわけではなく、数値を大きくしつつループさせるだけのコードでお茶を濁す。
# 自分用メモ
$ \mathrm{e} = \lim_{n \to \infty} ( 1 + \frac {1} {n} )^n $
この数値は複利の計算を発端として作られたとか。
年利10%で1年複利なら、年に10%増える。それが6ヶ月複利なら、半年後に5%増えて、次はその5%が入った分で5%計算されるので10.25%。四半期に1度になると、1度目は2.5%、2度目は5.026%、3度目は7.689...%で最後には10.381..%。
こんな風に徐々に大きくなるけど、最終的には上げ幅は縮小してネイピア数に収束することになる(らしい)。
数式の解説
eはネイピア数を指す時に用いられることがある。
limは極限。行くところまで行ったらこういう値になるよね的なヤツ。今回だとnが行くところまで行ったら、eはどういう値になるかな的な意味になる。無限に増えていってもどこかに収束するような式によく出てくる。nが無限に増えたらeも無限に増えます的な式ではあまり出てこない。
コードに直す
とりあえずnの値を0〜9まで1ずつ増やしていって、どういった値になるかを計算してみる。
function f( n:: Int ) (1 + 1 / n) ^ n end for n = 0:9 println( "$(n) : $(f(n))" ) end
当該の計算をしてくれる関数「f」を用意して、0〜10までの数値を引数に渡し、結果をprintしている。
出力結果。
0 : 1.0 1 : 2.0 2 : 2.25 3 : 2.37037037037037 4 : 2.44140625 5 : 2.4883199999999994 6 : 2.5216263717421135 7 : 2.546499697040712 8 : 2.565784513950348 9 : 2.5811747917131984
徐々に上げ幅を減少させながら増加している。
じゃ、これは結局いくつに収束するのか。Juliaに定数として設定されている値を見てみる。
# eで定義されてる print( e ) #=> e = 2.7182818284590... # euにもaliasが貼ってある print( eu ) #=> e = 2.7182818284590... # もっと深くまで見てみる print( big(e) ) #=> 2.718281828459045235360287471352662497757247093699959574966967627724076630353555e+00 with 256 bits of precision
とりあえず2.718くらいになるらしい。
本当にそうなるか、桁溢れしないように2の30乗の数値でやってみる。
print( f(2^30) ) #=> 2.7182818271932465
2.71828182まで一致した。64bit浮動小数点でやってるので限界はあるけど、無限に増やしていければもっと近づくことになる。
plotしてみる
実際に0〜2の10乗までの結果をplotしてみて、結果が収束していってるところを見てみる。
plotにはWinstonを使う。
Pkg.add( "Winston" ) import Winston Winston.fplot(x->(1 + 1 / x) ^ x, [0, 20])
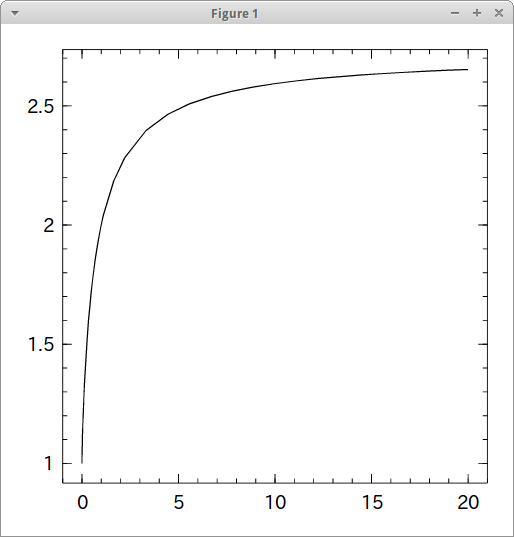
0〜20をplotするとこんな感じ。20の時点で2.653までいってる。