確率的最急降下法
概要
文系プログラマが機械学習エンジニアになるべく、数式をコードに直す試みをちまちまと続ける企画。
今回は確率的最急降下法。ニューラルネット的な処理でもよく出てくるので、一度は書いて置きたい子である。ソースコードは今日も元気にJuliaを利用。
@Versions Julia0.4.3
数式
Wikipedia の確率的勾配降下法の項より拝借。
# 自分用メモ
$ w \coloneqq w - \eta \nabla Q(w) = w - \eta \sum\limits_{i=1}~n \nabla Q_i(w) $
Q(w)を最小化するようなwを求めるのが目的。
η (イータ)はステップサイズ(学習率)。1回の学習でどの程度パラメータを動かすかを決める。適当な値を手動設定する。
∇(ナブラ)はベクトル。ロマンシング・サガをやってる人は詳しいはず。
Σ(シグマ)は合計。
つまり Q(w)の ベクトルの合計に、ηを掛けた値をペナルティにしてwから引けばいいのだと思う。たぶん。
コードに直す
とりあえずものすごく単純な例として、f(x) = (x + 2) ^ 2 という式があった場合に、yが最小になるxを求めるようなコードを書いてみる。
初期値はランダムに適当な場所(0〜3の間)を取って、ステップサイズは適当に0.1としておく。
function gradient_descent()
# ステップサイズは0.1としておく
η = 0.1
# 対象のデータは二次関数で
f(x) = (x + 2) ^ 2
# ランダムな初期値
x = rand()
# 最大で10000回までループしてポイント移動
arr::Array{Float64,1} = []
for i = 1:10000
penalty = η * f(x)
penalty < 1e-6 && break
x -= penalty
push!(arr, x)
end
return arr
end
式が (x + 2) ^ 2 なので、x = -2の時に0になる。最低値を取るだけでなく、値の変動を配列で記録している。
arr = gradient_descent() length(arr) #=> 3151 arr[end] #=> -1.9968378021783864
-2.0に近いところで終了している。正しく動いてくれたようだ。あまり良い例ではないけど、イメージ的にはこういうことで良いのだろう。たぶん。
確認作業
値がどう変動したかをグラフで確認。
import Winston Winston.plot(arr) Winston.plot(0:length(arr)-1, arr)
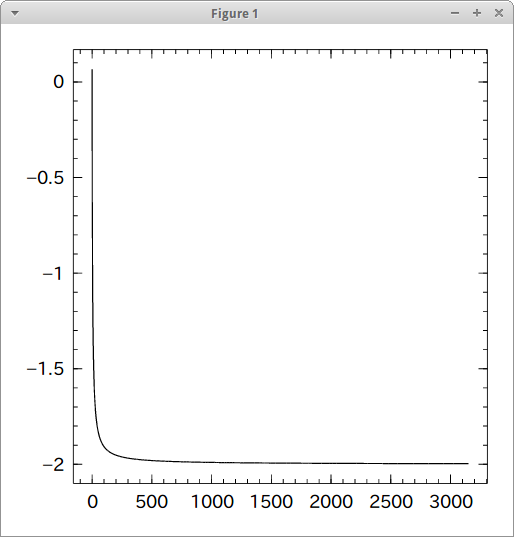
-2に向かって急激に近づき、その後は徐々に接近し、変動幅が閾値を下回ったところで終了していることがわかる。η = 0.1 と小さめに設定していたが、これを0.3とかにすると収束までにかかる至高回数がだいぶ減った。(3151 → 1817)
ηを大きくし過ぎると結果がInfになってしまった。負の値にも使えなかったり適当感が満載な処理になっている。
回帰してみる
実際に使用する際は複数の次元を持つ値に対して回帰するような用途が多いので、適当な値をでっち上げて回帰してみる。
とりあえず値のでっち上げから。
f(x) = 1.5x + rand() * 50 x = 1:100 y = map(f, x) Winston.scatter(x, y)
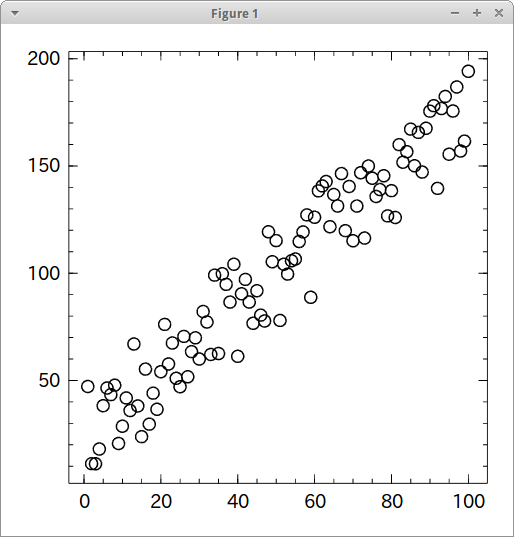
このデータに対して実行する。biasはrand() * 50なのでだいたい25くらいの値になるはず。coef=1.5, bias=25と出れば正解。
複数の項を持つ場合は、transposeしてlossを掛けてあげるとそれっぽいペナルティが出せるらしい。
function gradient_descent(x, y, η=0.0005)
# biasを追加
x = hcat(x, ones(100))
# 適当な初期値
w = rand(2)
# 10000回を上限にループして探索
for i = 1:10000000
loss = (x * w - y)
abs(sum(loss)) < 0.1 && break
w = w - η * (transpose(x) * loss) / length(x[1:end, 1])
end
return w
end
gradient_descent(1:100, map(f, 1:100))
#=> 1.46317
#=> 26.7898
ちょっとずれたけど乱数を大きめにしてるのでこんなもんだと思われる。