最小二乗法（一次）

概要

文系プログラマが数式アレルギーを治す為に、中学〜高校レベルの知識でもわかる数式を、プログラムのコードに直す作業を黙々と続ける企画。

ソースコードはJuliaを利用。LLVM（アイコンのワイバーンがこの手のアイコンらしからぬかっこよさ）ベースのJITコンパイラが速さの秘訣なJuliaを利用。

今回のテーマは最小二乗法の一次方程式版。二次も見てみたけど裸足で逃げ出したくなったので一次で。

数式

式はWikipediaの最小二乗法を参考にした。

http://ja.wikipedia.org/wiki/%E6%9C%80%E5%B0%8F%E4%BA%8C%E4%B9%97%E6%B3%95

求めたいのは下記のような方程式の「a」と「b」。

$f\left(x\right)=ax+b$

で、これを求める為の式が、下記になるらしい。

$a=\genfrac{}{}{0.1ex}{}{n{\displaystyle \sum _{k=1}^n}{x}_k{y}_k-{\displaystyle \sum _{k=1}^n}{x}_k{\displaystyle \sum _{k=1}^n}{y}_k}{n{\displaystyle \sum _{k=1}^n}{x}_k^2-{\left({\displaystyle \sum _{k=1}^n}{x}_k\right)}^2}$

$b=\genfrac{}{}{0.1ex}{}{{\displaystyle \sum _{k=1}^n}{x}_k^2{\displaystyle \sum _{k=1}^n}{y}_k-{\displaystyle \sum _{k=1}^n}{x}_k{y}_k{\displaystyle \sum _{k=1}^n}{x}_k}{n{\displaystyle \sum _{k=1}^n}{x}_k^2-{\left({\displaystyle \sum _{k=1}^n}{x}_k\right)}^2}$

# 自分用メモ
$ a = \frac {n \sum \limits_{k=1}^n x_k y_k - \sum \limits_{k=1}^n x_k \sum \limits_{k=1}^n y_k} {n \sum \limits_{k=1}^n x_k^2 - (\sum \limits_{k=1}^n x_k)^2} $
$ b = \frac {\sum \limits_{k=1}^n x_k^2 \sum \limits_{k=1}^n y_k - \sum \limits_{k=1}^n x_k y_k \sum \limits_{k=1}^n x_k} {n \sum \limits_{k=1}^n x_k^2 - (\sum \limits_{k=1}^n x_k)^2} $

長い。出てくる記号がΣだけなので難しくはないのだけど、書き写してて疲れた。MathMLに変換したら200行以上になった。

数式の解説

Σ（シグマ）は集合の総和。

今回のだと配列を2乗して全部足せとか、配列のxとyの各要素を掛け合わせろとかいった意味のものが複数含まれている。これで残差を二乗した和が最小になる値が求まるということだろうか。言われてみればそんな気もしなくもなくもない。

コードに直す

これをコードに直してみる。まずは試すデータから用意。

# 利用するデータ
arr = [ [0 0.2], [1.1 1], [2 2.3], [2.8 3], [4. 4.05], [5.1 4.9] ]

# 散布図を出してみる
import Winston
Winston.scatter( arr[:, 1], arr[:, 2], color="red" )
Winston.xlim( -0.1, 5.5 )
Winston.ylim( -0.1, 5.5 )

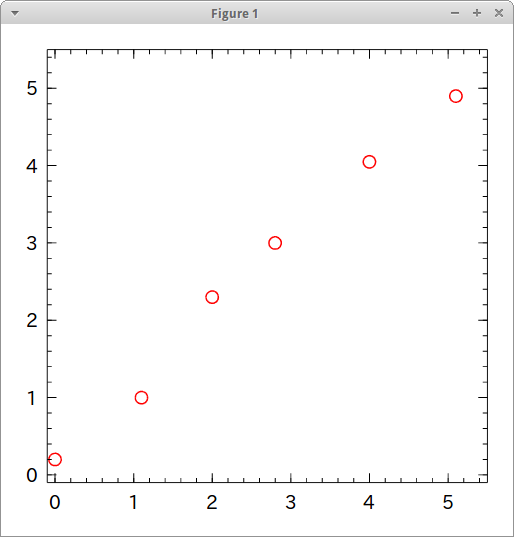
上記のようないかにも線が引きやすそうな二次元配列を引数に取って、切片と傾きを返してくれることをイメージする。

function least_square_method( arr:: Array{Float64, 2} )
  n = length( arr[:, 1] )
  # aの分母のとこ
  a1 = n * foldl( (x, y) -> x + y ^ 2,  arr[:, 1] ) - sum( arr[:, 1] ) ^ 2
  # aの分子のとこ
  a2 = n * sum( map( x -> arr[x, 1] * arr[x, 2], 1:length(arr[:, 1] ) ) ) - sum( arr[:, 1] ) * sum( arr[:, 2] ) 

  # bの分母のとこはaの分母と同じ
  b1 = a1
  # bの分子のとこ
  b2 = foldl( (x, y) -> x + y ^ 2,  arr[:, 1] ) * sum( arr[:, 2] ) - sum( map( x -> arr[x, 1] * arr[x, 2], 1:length(arr[:, 1] ) ) ) * sum( arr[:, 1] )

  # 戻り値
  a2 / a1, b2 / b1
end

さて、呼び出してみよう。

least_square_method( arr )
  #=> (0.9490318906605919,0.2024202733485205))

1.0, 0くらいを想定した配列だったので、割とそれっぽい数値になってる。

結果を確認する

戻ってきた値でplotしてみる。

coef, inspect = least_square_method( arr )

import Winston
Winston.hold(false)
Winston.scatter( arr[:, 1], arr[:, 2], color="red" )
Winston.hold(true)
Winston.fplot( x -> coef * x + inspect, [0, 5], color="blue" )

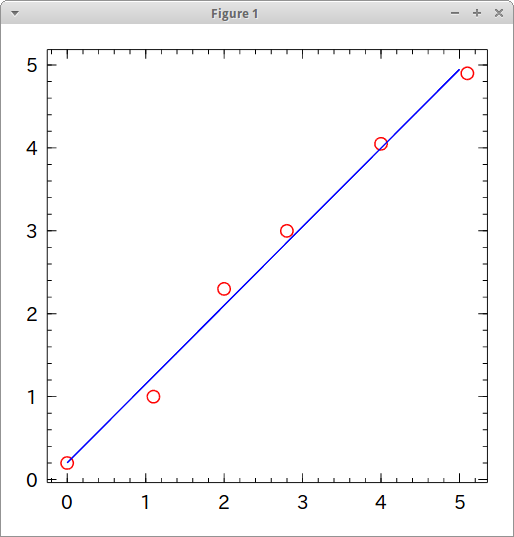
いい感じですね。

念の為、別の配列でも試してみる。今度は切片が3くらいで始まって、傾きが0.5くらいになるように。

arr = [ [0 3.2], [1.1 3.5], [2 3.8], [2.8 4.6], [4. 5.1], [5.1 5.5] ]
coef, inspect = least_square_method( arr )
  #=> (0.48576309794988637,3.068925588458618)

Winston.hold(false)
Winston.scatter( arr[:, 1], arr[:, 2], color="red" )
Winston.hold(true)
Winston.fplot( x -> coef * x + inspect, [0, 5], color="blue" )
Winston.ylim(0, 7)

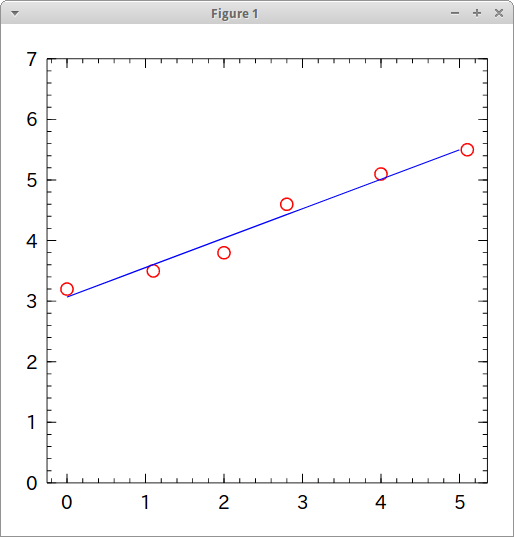
オッケーですね。

実はこれを出すまでに3回くらい式に誤りがあって書き直しました。式が複雑になってくると移植するだけでも大変。