対数正規分布

概要

文系プログラマが数式アレルギーを治す為に、中学〜高校レベルの知識でもわかる数式を、プログラムのコードに直す作業を黙々と続ける企画。

ソースコードはJuliaを利用。

今回は対数正規分布。

数式

式はWikipediaの対数正規分布を参考にした。

https://ja.wikipedia.org/wiki/%E5%AF%BE%E6%95%B0%E6%AD%A3%E8%A6%8F%E5%88%86%E5%B8%83

こんな感じ。

$f\left(x\right)=\genfrac{}{}{0.1ex}{}{1}{\sqrt{2\pi }\sigma x}{e}^{-\genfrac{}{}{0.1ex}{}{{(\ln x-\mu )}^2}{2{\sigma }^2}},0<x<\infty$

# 自分用メモ
$ f( x ) = \frac { 1 } { \sqrt { 2 \pi } \sigma x } e ^ { - \frac { ( \ln x - \mu ) ^ 2 } { 2 \sigma ^ 2 } }, { 0 < x < \infty } $

正規分布と比べて、eやlnが増えている。対数だからね。

あとxは0を超える数値に限られている。

数式の解説

π（パイ）は円周率。

σ（シグマ）は標準偏差。(※ 実は違った。後述）

μ（ミュー）は平均。(※ 実は違った。後述）

eはネイピア数。

lnはeを底とする対数。

コードに直す

まずはとある集合に対して平均μと標準偏差σを出す。

a = [3.0, 2.5, 1.4, 6.2, 3.3, 2.1, 5.0]

μ = mean( a )
  #=> 3.3571428571428577
σ = std( a )
  #=> 1.6860774427223513

次に1 / √2π σxのところを書く。

1 / ( √(2π) * σ  * x )

次にexpの中。

- ( (log(x) - μ) ^ 2 ) / ( 2σ ^ 2 )

これを合わせると、こんな風になる。

f(x) = (1 / ( √(2π) * σ  * x ) ) * e ^ ( - ( (log(x) - μ) ^ 2 ) / ( 2σ ^ 2 ) )

plotしてみる

とりあえずplotしてそれっぽい形になっているか確認してみる。

a = [3.0, 2.5, 1.4, 6.2, 3.3, 2.1, 5.0]
μ = mean( a )
σ = std( a )
f(x) = ( 1 / ( √(2π) * σ  * x ) ) * ( e ^ ( - ( (log(x) - μ) ^ 2 ) / ( 2σ ^ 2 ) ) ) 

import Winston
Winston.fplot( f, [0.0, 10.0] )

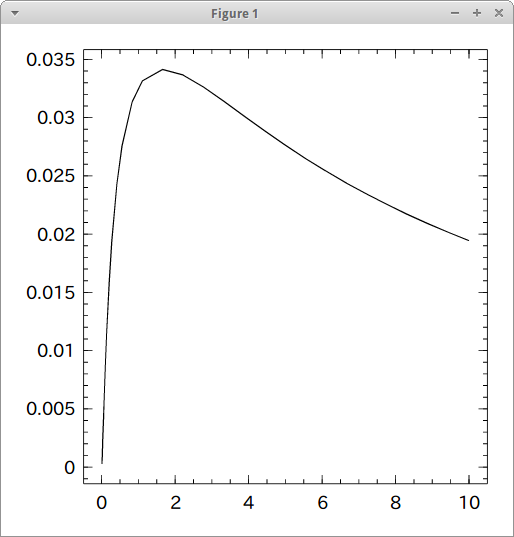
なんか違くね？

調べてみると対数正規分布においてμとσはmeanとstdで出すものではないようだ。Wikipediaに出てるグラフもμ=0の分布が書かれてるんだからそりゃそうだよな。

取り急ぎ、英語版Wikipediaに載ってた式でμとσを出し直す。

a = [3.0, 2.5, 1.4, 6.2, 3.3, 2.1, 5.0]
mu(a) = log(mean(a) / √(1 + var(a)/mean(a)^2))
sigma(a) = √(log(1 + var(a) / mean(a)^2))

μ = mu(a)
σ = sigma(a)

f(x) = ( 1 / ( √(2π) * σ  * x ) ) * ( e ^ ( - ( (log(x) - μ) ^ 2 ) / ( 2σ ^ 2 ) ) ) 

import Winston
Winston.fplot( f, [0.0, 10.0] )

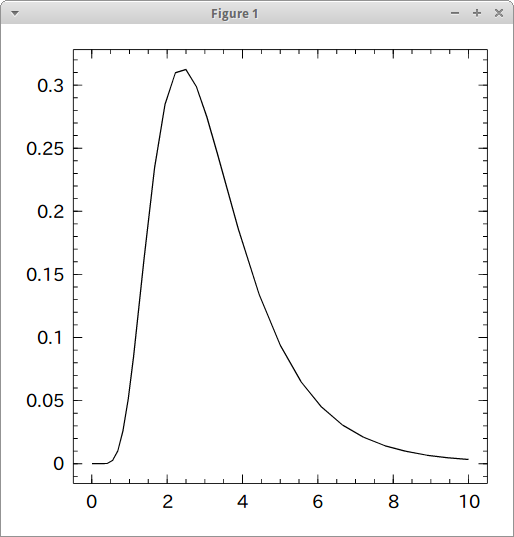
そうそう、こんな感じ。

答え合わせ

JuliaのDistributions.jlを使って答え合わせしてみる。

import Distributions
Distributions.pdf( Distributions.LogNormal( μ, σ ), 1.0 )
  #=> 0.057503676565648795

f(1.0)
  #=> 0.057503676565648795

Distributions.pdf( Distributions.LogNormal( μ, σ ), 2.0 )
  #=> 0.29183226612953866

f(2.0)
  #=> 0.29183226612953866

完全に一致。