正規分布（累積分布）

概要

文系プログラマが数式アレルギーを治す為に、中学〜高校レベルの知識でもわかる数式を、プログラムのコードに直す作業を黙々と続ける企画。

ソースコードはJuliaを利用。デフォルトで√2xとか書けるところがお気に入りのJuliaを利用。

前回は正規分布の確率密度関数（= Probability Density Function = PDF）の方をやったので、今回は累積分布関数（= Cumulative Distribution Function = CDF）の方。

数式

式はWikipediaの正規分布を参考にした。

http://ja.wikipedia.org/wiki/%E6%AD%A3%E8%A6%8F%E5%88%86%E5%B8%83

こんな感じ。

$\genfrac{}{}{0.1ex}{}{1}{2}[1+erf\left(\genfrac{}{}{0.1ex}{}{x-\mu }{\sigma \sqrt{2}}\right)]$

# 自分用メモ
$ \frac {1} {2} [ 1 + erf( \frac { x - \mu } { \sigma \sqrt 2 } ) ] $

erfが出てくる以外は普通の式。そして今回、erfはJuliaの関数に任せるので（このへんやりだすと高校数学レベル超えそうなので）、面倒なことは特になく算出できる予定。

数式の解説

erfは誤差関数。

σ（シグマ）は標準偏差を意味することが多い。

μ（ミュー）は平均を意味することが多い。この場合は算術平均。

コードに直す

とりあえず適当な配列に対して、平均と標準偏差を出しておく。

a = [3.0, 2.5, 1.4, 6.2, 3.3, 2.1, 5.0]

μ = mean( a )
  #=> 3.3571428571428577
σ = std( a )
  #=> 1.6860774427223513

erf関数はJuliaでは既に用意されている。Pythonの場合はscipy.special.erfとか。

f(x) = 1/2 * ( 1 + erf( (x - μ) / (σ * √2) ) )

誤差関数を人任せにしたお陰でだいぶ簡潔なコードで済んだ。近似式使って自前でやった方が良かったのかな。でも誤差の分、結果変わっちゃうしな。

とりあえず±1.96σにおける数字でも見てみる。

f( μ + 1.96σ ) - f( μ - 1.96σ )
  #=> 0.950004209703559

合ってるか確認

さて、この式が正しいかどうか確認してみる。今回はSciPyに頼らずJuliaの Distributions.jl を利用。

まずは自作の関数でplotしてみる。描画する区間はμ - 3σ 〜 μ + 3σ とする。±3σなので99.73%くらいが含まれる図になるはず。

f(x) = 1/2 * ( 1 + erf( (x - μ) / (σ * √2) ) )

import Winston
Winston.fplot( f, [μ - 3σ, μ + 3σ] )

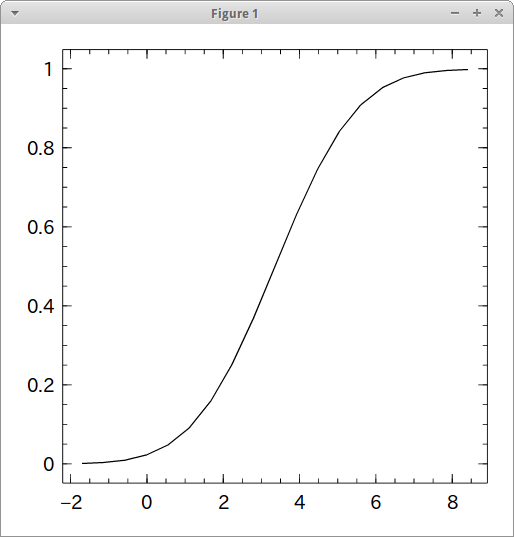
それっぽい形になっている。じゃ、次はDistributions.jlで同様の処理を行ってみる。

Pkg.add( "Distributions" )
import Distributions

norm = Distributions.Normal( μ, σ )
f(x) = Distributions.cdf( norm, x )
f( μ + 1.96σ ) - f( μ - 1.96σ )
  #=> 0.950004209703559

import Winston
Winston.fplot( f, [μ - 3σ, μ + 3σ] )

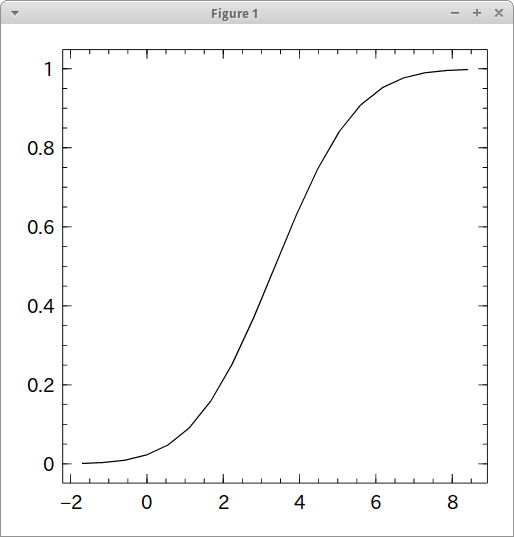
まったく同じ結果になりました。めでたし。