ポアソン分布

概要

文系プログラマが数式アレルギーを治す為に、中学〜高校レベルの知識でもわかる数式を、プログラムのコードに直す作業を黙々と続ける企画。

ソースコードはJuliaを利用。ccallとPyCallを使えばなんとかなるさなJuliaを利用。

今回のテーマはポアソン分布。人の恋路を邪魔するヤツは、馬に蹴られるポアソン分布。

数式

式はWikipediaのポアソン分布を参考にした。

http://ja.wikipedia.org/wiki/%E3%83%9D%E3%82%A2%E3%82%BD%E3%83%B3%E5%88%86%E5%B8%83

こんな感じ。

$P(X=k)=\genfrac{}{}{0.1ex}{}{{\lambda }^k{\mathrm{e}}^{-\lambda }}{k!}$

# 自分用メモ
$ P( X = k ) = \frac { \lambda ^ k \mathrm{e} ^ {-\lambda} } { k! } $

これで馬に蹴られる確率を測れるらしい。階乗が出てきてλとかがいるけど、λ自体はただの変数なので、それほど面倒なところはない。

しかしこういう確率がネイピア数とかから取れるとか、世の中はよくわからない仕組みになってるものだ。

数式の解説

確率変数Xはパラメータλのポアソン分布に従うという意味の式らしい。詳しくはWikipedia参照（丸投げ）。

λ（ラムダ）はここではただの変数。平均するとその期間に何回発生する的な数値が入る。

kはその事象が起こる回数。

eはネイピア数。

コードに直す

じゃ、とりあえず関数だけコードにしてみる。

仮に「平均で日に3回起こる」とされている事象が、「1日に3回起こる確率」は何%かを測ってみる。

慣れてきたので階乗の計算にはreduceを使ってみようかと思った。例えば1〜nの階乗を取る場合は、下記のようになる。1〜nのRangeに対して、順に掛け合わせていくという意味になる。

n = 5
reduce( (x, y) -> x * y, 1:n )
  #=> 120

こんな感じの記述とだいたい同じ意味。

# 階乗を取る関数
n = 5
fact = 1
for i = 1:n
  fact *= i
end
fact
  #=> 120

じゃ、階乗はこれを使って、kを与えると確率が返る関数を書いてみる。

# 年に3回起こる事象だとする
λ = 3

# 階乗を取る関数（nが0の場合は1にする）
fact = n -> n == 0 ? 1 : reduce( (x, y) -> x * y, 1:n )

# 確率を出す関数
f = k -> ( λ ^ k ) * ( e ^ (-λ) ) / fact( k )

# kが3になる確率
f(3)
  #=> 0.22404180765538775

# kが0になる確率
f(0)

ということで、1日に3回起こる事象が実際に3回起こる確率は、22.4%とされた。

せっかくなので0〜20回までの発生率をグラフにしてみよう。

# 0〜20までの数値をPython使い風にリスト内包表記で取る
# WinstonにFloat型のArrayで渡さないといけないので変換もしておく
x = 0:20
y = float( [ f(i) for i = x ] )

import Winston
Winston.plot( x, y )

こんな風になった。

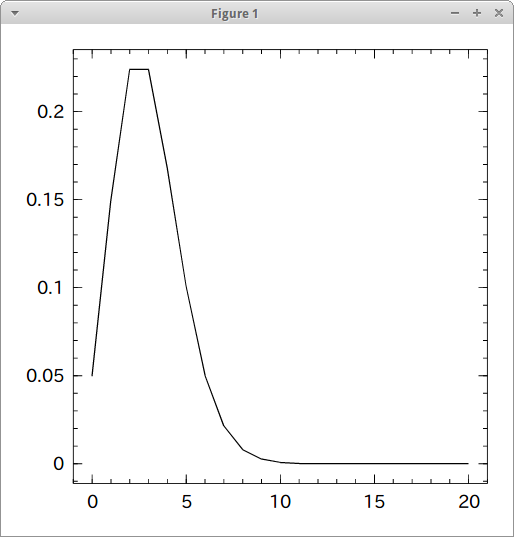
合っているか確認する

本当にこれで合ってるのか不安なので、SciPyのpoissonで出力される値と同数になっているか比べてみる。

まずは今回自作した関数で、λ=3, k=0〜5の数字を見てみる。

λ = 3
for i = 0:5
  println( "$(i) : $(f(i))" )
end
  #=> 0 : 0.049787068367863944
  #=> 1 : 0.14936120510359183
  #=> 2 : 0.22404180765538775
  #=> 3 : 0.22404180765538775
  #=> 4 : 0.16803135574154082
  #=> 5 : 0.10081881344492448

2と3の時に約22.4%。5の時は約10%。

次にSciPyの場合。PyCallから呼ぼうと思ったけどうまくいかなかったので、誠に遺憾ながらPythonで実行。

import scipy as sp
lamb = 3
for i in range(0, 6):
  print( '{0} : {1}'.format(i, sp.stats.poisson.pmf( i, lamb )) )
  #=> 0 : 0.0497870683679
  #=> 1 : 0.149361205104
  #=> 2 : 0.224041807655
  #=> 3 : 0.224041807655
  #=> 4 : 0.168031355742
  #=> 5 : 0.100818813445

桁が違うのは置いておいて、自作の関数とちゃんと同じ数字を返してくれている。