シグモイド関数

概要

文系プログラマが機械学習エンジニアになるべく、数式をコードに直す試みをちまちまと続ける企画。

今回はロジスティック回帰なんかでも出てくるシグモイド関数。sigmoid（S字）という意味からわかる通り、鈴鹿のS字コーナーのような形をしたカーブを描く。

数式

WikipediaのSigmoid functionの項より拝借。

$S\left(t\right)=\genfrac{}{}{0.1ex}{}{1}{1+e^{-t}}$

# 自分用メモ
$ S(t) = \frac {1} {1 + e^{-t}} $

eはネイピア数。

けっこう簡単な式。

コードに直す

今回はとても簡単。

S(t) = 1 / (1 + e ^ -t)

これだけ。

確認作業

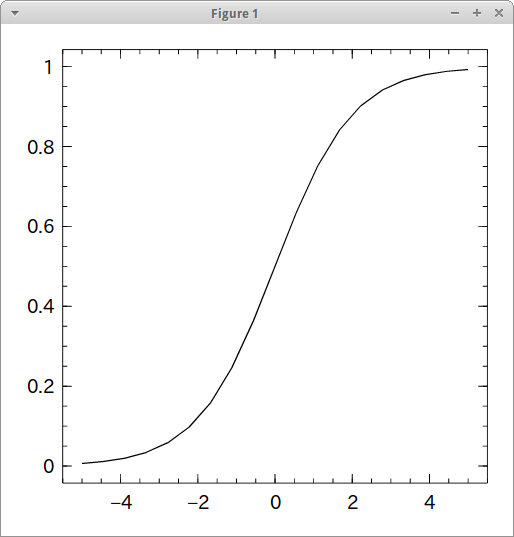
グラフで-5〜+5の区間を描画してみる。

import Winston
Winston.fplot(S, [-5, 5])

ちゃんとS字型になってる。

expを使う

S(t) = 1 / (1 + e ^ -t) で計算したけど、巷の参考コードを見ていると S(t) = 1 / (1 + exp(-t)) としている例が多い。

S1(t) = 1 / (1 + e ^ -t)
S2(t) = 1 / (1 + exp(-t))

S1(1.23)
  #=> 0.7738185742694538
S2(1.23)
  #=> 0.7738185742694538