標準正規分布

概要

文系プログラマが数式アレルギーを治す為に、中学〜高校レベルの知識でもわかる数式を、プログラムのコードに直す作業を黙々と続ける企画。

ソースコードはJuliaを利用。PythonとRubyの間くらいの書き方ができるJuliaを利用。

今回のテーマは標準正規分布。ただの正規分布にしようかと思ったけど、アレルギー反応が現れたので簡単な方から順に行くことにした。

@CretedDate 2014/12/29
@Versions Julia0.3.3

今回利用する式は確率密度関数のヤツ。Wikipediaの正規分布を参考にした。

こんな感じ。

$f (x) = \frac{1}{\sqrt{2 π}} \exp (- \frac{x^{2}}{2})$

初回と比べるとだいぶ難しくなってきた。けど、ΣΣΣとか∬∬∬とか言われているわけではないので、落ち着いて読めばちゃんとわかる。

この式は、平均が0、標準偏差が1の正規分布（標準正規分布）での確率密度関数で、これを関数に直すと、標準正規分布の時にxがどの程度の確率で現れるかを知ることができる。

# 自分用メモ
$ f(x) = \frac {1} { \sqrt {2 \pi} } \exp(- \frac {x^2} {2}) $

π（パイ）はご存知の通り円周率。

f(x)はプログラマ的には、xを引数に取る関数として考えると馴染み深い。

expは指数関数。exponential function。ネイピア数を底に取るやつ。

Juliaのコードに直す。

Juliaの場合、πとかが既に設定されているので、コードの前半（expより前の部分）は下記のように書ける。

# expより前の部分の式相当
1 / sqrt( 2 * π )

これにexp以降を掛ければ良いので、合わせると下記のようになる。

# fというxを引数に取る関数を設定
f = x -> 1 / sqrt( 2 * π ) * exp( - ( x ^ 2 ) / 2 )

これでf(x)が書けた。

f(x)を使って -3.0〜3.0 の区間をplotしてみる。

import Winston
Winston.fplot( f, [-3.0, 3.0] )

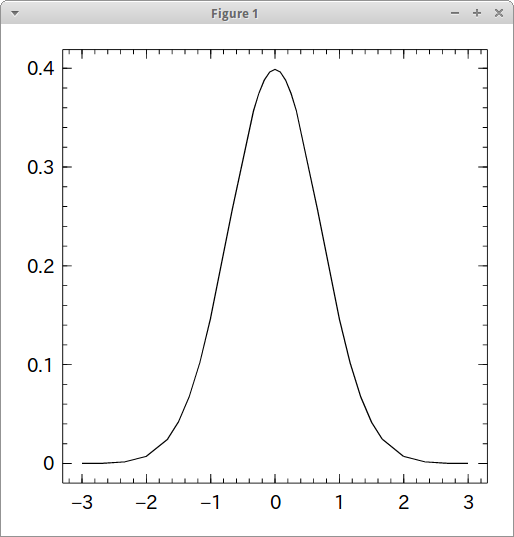
標準正規分布

見慣れた曲線が出てきた。これを使って面積を計算すると、指定区間の確率が出せるそうな。

確率密度関数がわかったので、試しにゴリ押しで確率を出してみる。

よく出てくる数字として、標準偏差×±1.96区間が95%になるという数値にある程度近いものが出るか確認してみる。

0〜1.96までの区間を1/100万ずつに区切って面積を出していけば、それなりに近い値になるはず。

d = 1e6
y = 0.0
for i = 0:(d * 1.96)
  y += f(i / d) * (1 / d)
end

y * 2
  #=> 0.95000466708674

0 〜 1.96 までの数値を出して、その後、0 〜 -1.96 の値を追加する為に×2をしている。

適当な計算の割には、まずまずそれっぽい数値になっている。