statsmodelsで多次元とか多項式の最小二乗法

サンプルデータについて

国勢調査から、1953〜1973年の労働力人口をに関する数値を取得して利用してみる。（単位は万人）

http://www.stat.go.jp/data/roudou/longtime/03roudou.htm

これを適当にコピペして数値の部分だけテキストファイルに貼り付ける。ついでに適当なヘッダも書き加える。

population
3788
3698
3935
3982
4076
4105
4086
3996
・
・
・

これをplotすると下記のようになる。

import statsmodels.api as sm
import pandas as pd
df = pd.read_csv( 'foo.txt' ).reset_index()
df.population.plot()

plot

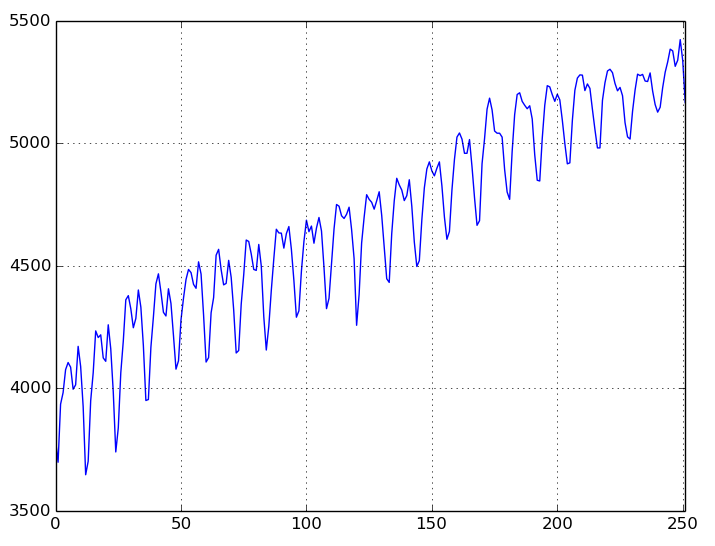
右肩上がり。但し春から夏にかけて増加し、冬は下がるという傾向があるようだ。

OLSで線形回帰

まずは二次元で単純な線形回帰から。

model = sm.OLS( df.population, df.index ).fit()
model.params
  #=> x1    29.288508

ただXとYを渡すだけだと、coefしか返ってこない。interceptがない。

この結果でlineを引いてもこんな感じ。

import matplotlib.pyplot as plt
df.population.plot()
plt.plot( [0, 250], model.predict( [0, 250] ) )

plot

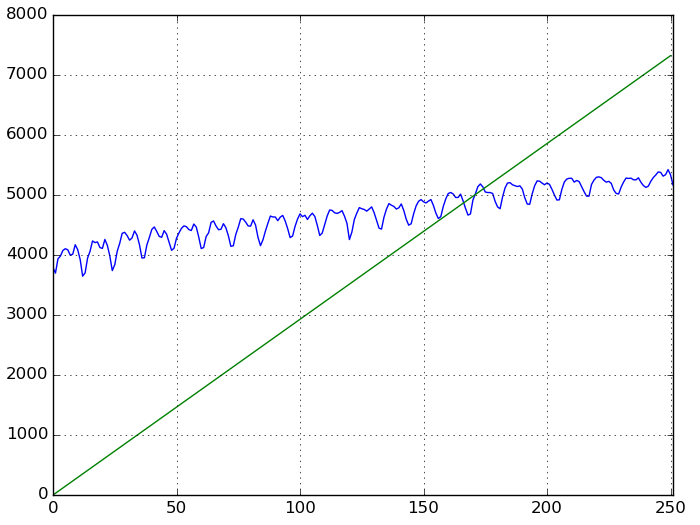
これではアカンのでadd_constantして切片を付ける。

model = sm.OLS( df.population, sm.add_constant( df.index ) ).fit()
model.params
  #=> const    4013.343654
  #=> x1          5.352065

constが追加された。

このモデルでplotするとこんな感じになる。

import matplotlib.pyplot as plt
df.population.plot()
plt.plot( [0, 250], model.predict( sm.add_constant([0, 250]) ) )

plot

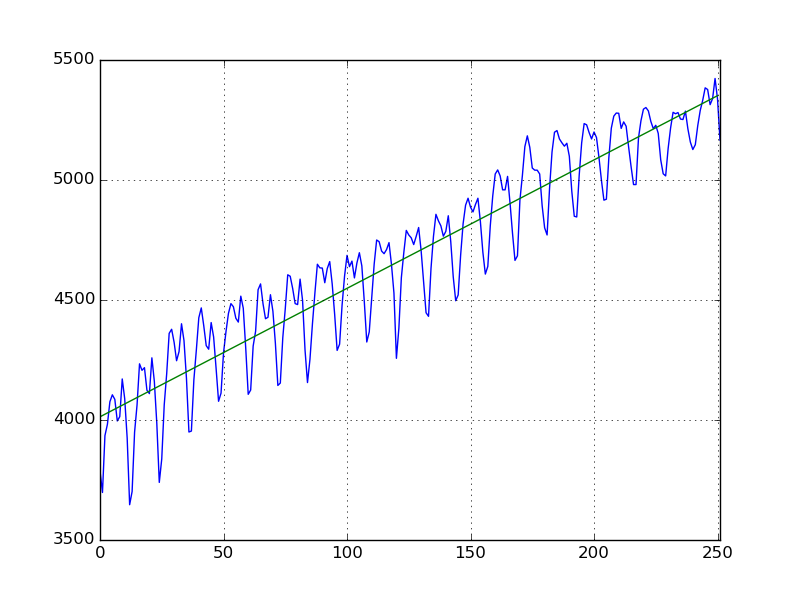
ベネ（良し）。そこそこ当てはまる感じになった。

OLSで三次元で回帰

前節ではX座標とY座標のみで計算したけど、年と月を分けて学習させればよりフィットしそうだよね、ということでデータを書き換えてみる。

yearとmonth（yearは初年度を0とする）のカラムを追加している。

year,month,population
0,1,3788
0,2,3698
0,3,3935
0,4,3982
0,5,4076
0,6,4105
0,7,4086
0,8,3996
0,9,4014
0,10,4171
0,11,4089
0,12,3925
1,1,3647
1,2,3702
1,3,3949
1,4,4063
1,5,4234
・
・
・

内容確認。

import statsmodels.api as sm
import pandas as pd
df = pd.read_csv( 'foo.txt' )
df.set_index(['year', 'month']).plot()

plot

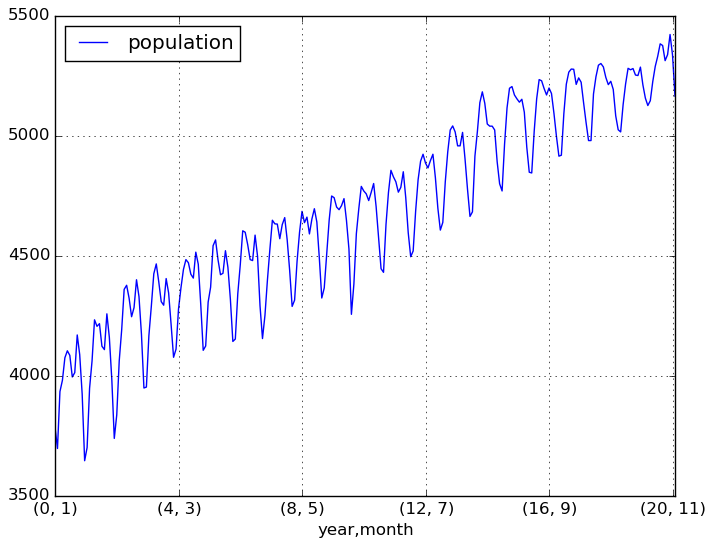
X軸のlabelのみ変化して数値は変わりなし。

ついでに3Dでplotしてみる（特に意味はない）。

import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

fig = plt.figure().gca(projection='3d')
fig.scatter(df.year, df.month, df.population)

plot

うん、きれいに出た（特に意味はない）。

じゃ、これでOLS。monthの変動は単純な線形では出せないと思うのだけど、とりあえずそのままで。

X = sm.add_constant( df[ ['year', 'month'] ] )
model = sm.OLS( df.population, X ).fit()
model.params
  #=> const    3900.012626
  #=> year       63.755303
  #=> month      22.686480

じゃ、これでplotしてみる。

まずはDataFrameに推測値を設定。fの中で[1, year, month]でpredictしてるけど、1はintercept。

f = lambda year, month: model.predict( [1, year, month] )[0]
df['p'] = df.apply( lambda x: f( x.year, x.month ), axis=1 )

推測値をpとしてDataFrameに入れた。あとはこれを実際の値と並べて表示する。

import matplotlib.pyplot as plt
df[ ['population', 'p'] ].plot()

plot

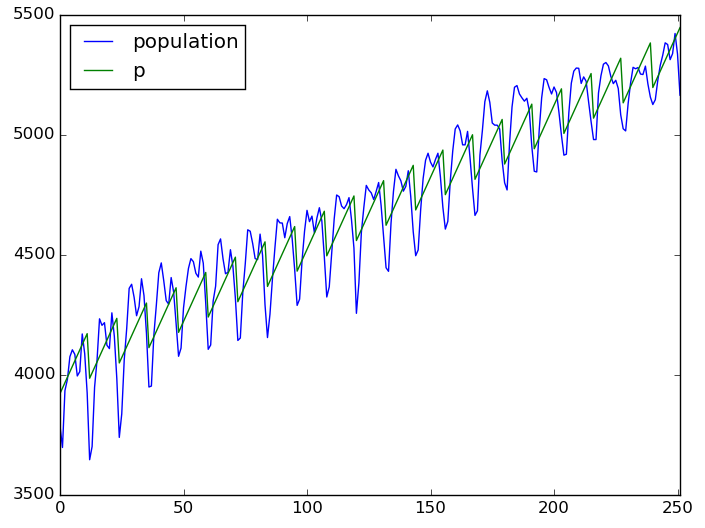
悪くはないけど良くもない。

月をそれぞれダミー変数的に扱う

前項のように単純にやると、12月が最大（実際の数値では6〜7月頃が最大）になってしまうので、月をそれぞれダミー変数として扱うことにする。

とりあえずmonth_1〜month_12までをDataFrameに追加。

for i in range(1, 13):
    df['month_%s' % i] = (df.month == i).astype(np.int)

yaerと追加したmonth_1〜month_12を使ってOLSにかける。

columns = ['year'] + [ 'month_%s' % i for i in range(1, 13) ]
X = sm.add_constant( df[ columns ] )
model = sm.OLS( df.population, X ).fit()
model.params
  #=> const       3736.130536
  #=> year          63.755303
  #=> month_1       26.268815
  #=> month_2       48.268815
  #=> month_3      230.125957
  #=> month_4      339.840243
  #=> month_5      440.078338
  #=> month_6      447.840243
  #=> month_7      422.745005
  #=> month_8      368.745005
  #=> month_9      381.221195
  #=> month_10     439.792624
  #=> month_11     363.506910
  #=> month_12     227.697386

いい感じに夏頃に高く冬にかけて低くなる係数が割り当てられている。

これをplotする。np.concatenateでinterceptの1とcolumns（yearとmonth1〜12が入ってる）を結合して、その値でpredictしている。

f = lambda row: model.predict( np.concatenate( ([1], row[columns].values) ) )[0]
df['p'] = df.apply( lambda row: f( row ), axis=1 )
df[ ['population', 'p'] ].plot()

plot

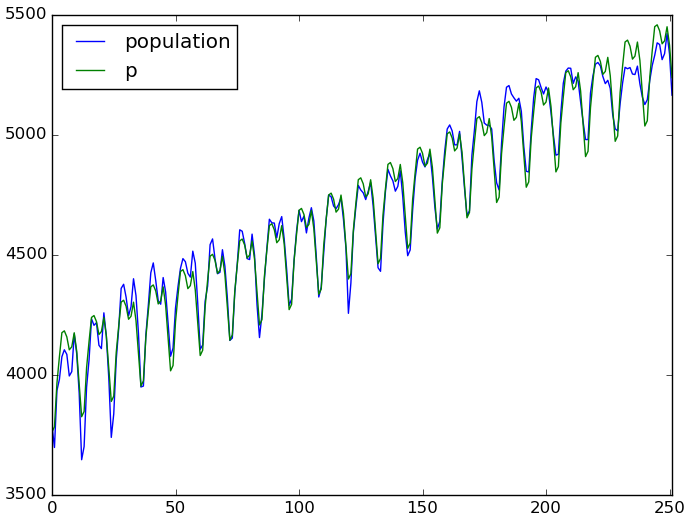
たいへん良いのではないでしょうか。

多項式を使ってみる

似たようなことを多項式でやってみる。

まずは夏頃が高くなるという特性を考えて、6〜7月が最大になるような式にしてみる。

多項式ではstatsmodels.apiではなく、statsmodels.formula.apiを利用する。

月の補正はとりあえずこんなんでいいか。（6.5月が最大となるような二次関数）

month = np.arange(1, 13, 1)
plt.plot( month, (6.5 - abs(6.5-month))**2 )

plot

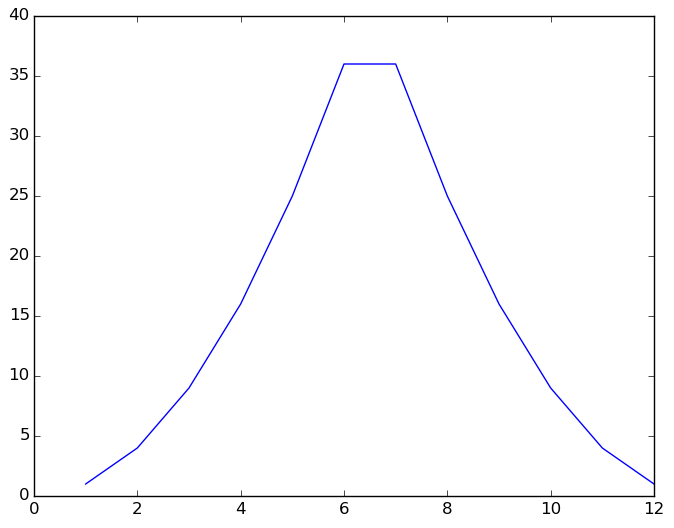
例的にax + by^2みたいなのとか、x / y みたいなのが出てくると良いのだけど、今回のサンプルデータだと使わなさそうなので、こんな感じで回帰させる。

import statsmodels.formula.api as smf
import pandas as pd
df = pd.read_csv( 'foo.txt' )

def f(month):
  return (6.5 - abs(6.5-month))**2

model = smf.ols( formula='population ~ year + f(month)', data=df ).fit()
model.params
  #=> Intercept    3925.743176
  #=> year           63.755303
  #=> f(month)        8.026257

できたモデルでplotしてみる。

df['p'] = model.predict( df )
df[ ['population', 'p'] ].plot()

plot

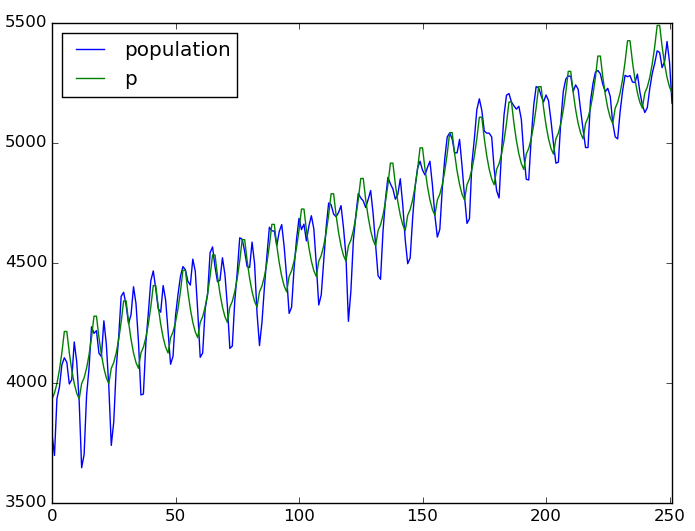
適当な式なのでそこまでキレイには合ってないけど悪くもない。

1/12してsin取るとよりキレイになりそうな気がする。

def f(month):
  return sin( month / 12.0 * pi )
model = smf.ols( formula='population ~ year + f(month)', data=df ).fit()
df['p'] = model.predict( df )
df[ ['population', 'p'] ].plot()

plot

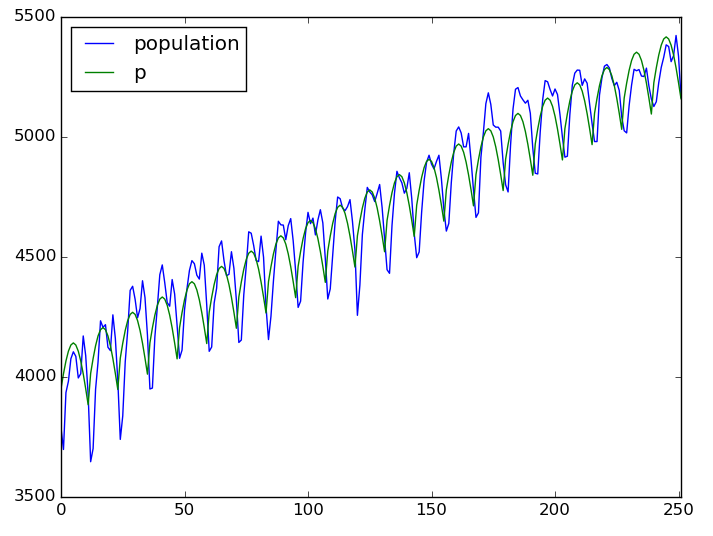
なかなか良いですね。

こうやってさらっとformulaの中に式がかけるのは大変便利。複雑な多項式でもさらっと書けそう。うまくフィットさせられるかは別として。

概要

サンプルデータについて

OLSで線形回帰

OLSで三次元で回帰

月をそれぞれダミー変数的に扱う

多項式を使ってみる